Markov Chain Monte Carlo in Portfolio Optimisation and Efficient Frontier Exploration

Constructing an optimal investment portfolio is a fundamental challenge in modern finance. Investors seek to balance risk and return, aiming to maximize their potential gains while minimizing the associated volatility.

Markov Chain Monte Carlo (MCMC), a powerful computational technique based on the idea that investors can optimize their portfolio by selecting a combination of assets that maximizes expected return for a given level of risk or minimizes risk for a given level of expected return. This is achieved by diversifying the portfolio across different assets and sectors, which helps to reduce the overall volatility and risk of the portfolio.

Computational method that can be employed to explore the efficient frontier - the set of optimal portfolios that offer the highest expected return for a given level of risk.

In this article, I will demystify MCMC, break it down into digestible chunks, and explore its real-world applications.

What is MCMC?

MCMC is a class of algorithms that use random sampling to simulate a Markov chain, a sequence of random variables where the probability of each variable depends only on the current state, not the entire history. By running the Markov chain for a sufficient number of iterations, MCMC can be used to generate samples from a target probability distribution, even if that distribution is complex or high-dimensional.

We can break down MCMC into 2 main components:

1. Markov Chains.

Each step depends only on the current position. Markov chains model systems where the future state relies solely on the present state.

2. Monte Carlo.

We simulate thousands of scenarios to estimate outcomes. MCMC is our technique, revealing hidden truths.

In the context of portfolio optimization, the target distribution is typically the joint distribution of asset returns, which can then be used to estimate the efficient frontier. MCMC allows us to sample from this distribution without making restrictive assumptions about the underlying asset returns, such as normality.

Practical Portfolio Optimization with MCMC

Let’s put theory into practice and explore real-world applications.

To illustrate the use of MCMC in portfolio optimization, consider the following example. Suppose we have a universe of 4 assets (MCD, IBM, AAPL, MSFT), and we want to find the optimal portfolio weights that maximize the portfolio's Sharpe ratio (the ratio of the portfolio's expected return to its standard deviation).

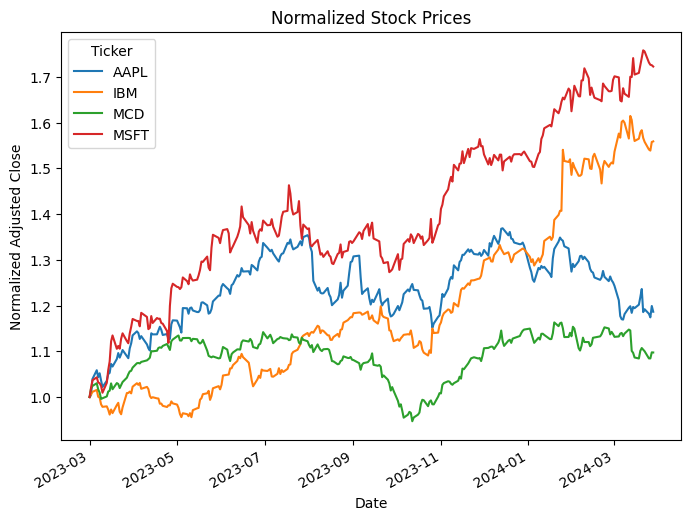
To compare performance of these 4 stocks and get the idea on their volatility, we can visualize their daily returns throughout the past year.

Using MCMC, we will follow these steps:

1. Specify the asset return model. Assume the asset returns follow a multivariate normal distribution with unknown mean and covariance matrix.


2. Define the target distribution. The target distribution is the joint distribution of the asset returns, which we can use to estimate the efficient frontier.


3. Run the MCMC algorithm. Initialize the Markov chain with random portfolio weights, and run the MCMC algorithm to generate samples from the target distribution. This involves repeatedly updating the portfolio weights based on the current state of the chain and the target distribution.

Run the Algorithm:

And get the sample Portfolio Allocations:

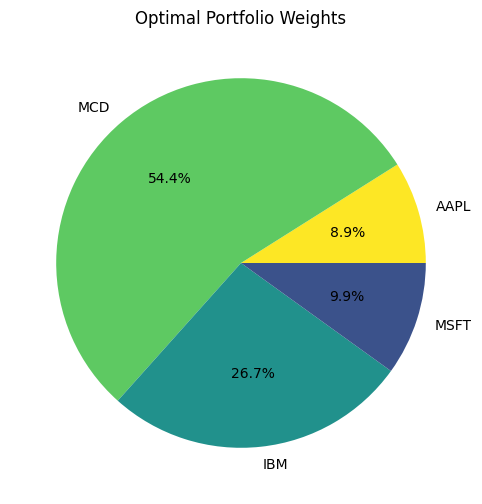
Estimate the efficient frontier.

By generating a large number of random portfolio weights and computing the corresponding returns and risks, we can map out the entire set of optimal portfolios. This is done by collecting all the portfolio return and risk samples, and then plotting them on a scatter plot.

The resulting visualization shows the efficient frontier - the curve that represents the set of portfolios that offer the highest expected return for a given level of risk. To highlight the optimal portfolio, we'll add a red dot to the plot, indicating the portfolio with the maximum Sharpe ratio.

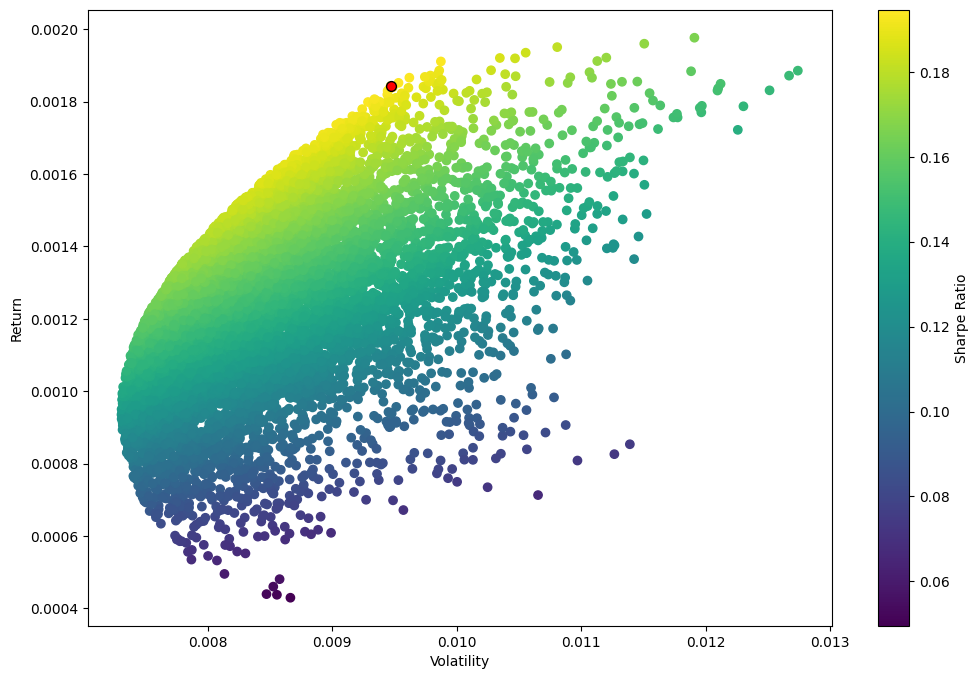
The efficient frontier is the hallmark of modern portfolio theory, representing the set of optimal investment portfolios that strike the perfect balance between risk and return. This frontier delineates the highest expected return attainable for a given level of risk, or conversely, the lowest risk achievable for a target level of expected return.

Portfolios that fall below the efficient frontier are considered sub-optimal, as they fail to deliver the maximum possible return for their associated risk profile. Investors seeking to optimize their investments cannot afford to overlook these underperforming portfolios, as they do not provide the requisite return to justify their risk exposure.

Conversely, portfolios that reside to the right of the efficient frontier are also deemed suboptimal, despite their higher expected returns. These portfolios exhibit a disproportionately elevated level of risk compared to the returns they generate, rendering them undesirable for risk-averse or risk-conscious investors.

The efficient frontier serves as a guiding light, illuminating the path to the most judicious allocation of investment capital. By firmly mapping out this frontier, investors can navigate the complex financial landscape with clarity, identifying the optimal mix of assets that aligns perfectly with their unique risk preferences and investment objectives.

Mastering the intricacies of the efficient frontier is a cornerstone of successful portfolio management, empowering investors to construct diversified, risk-adjusted portfolios that maximize their chances of achieving their long-term financial goals.