
Neural Networks in 5 Key Concepts for Understanding Their Functionality in Quantitative Finance
9 May, 2024
Neural networks, inspired by the intricate connections of the human brain, have become the backbone of modern artificial intelligence. These powerful models excel at tasks like image recognition, natural language processing, and recommendation systems. In this article, we'll delve into the fundamental concepts that underpin neural networks, demystifying their inner workings. Whether you're a beginner or an enthusiast, fasten your seatbelt as we explore the neural landscape!
Neural Networks in Quantitative Finance
In quantitative finance, neural networks are often used for time-series forecasting, constructing proprietary indicators, algorithmic trading, securities classification, and credit risk modelling. They have also been used to construct stochastic process models and price derivatives. Despite their usefulness, neural networks also face challenges in finance, including interpretability, overfitting, and data quality. As the field evolves, researchers continue to refine these models for better performance and reliability.
In this article, I will breakdown 5 important concepts of Neural Networks that will help you to understand how they work. By exploring these key concepts, you'll gain a deeper understanding of the inner workings and practical applications of neural networks, empowering you to harness their potential in your own work.
1. The Intricacies of Neural Networks. From Perceptrons to Deep Learning
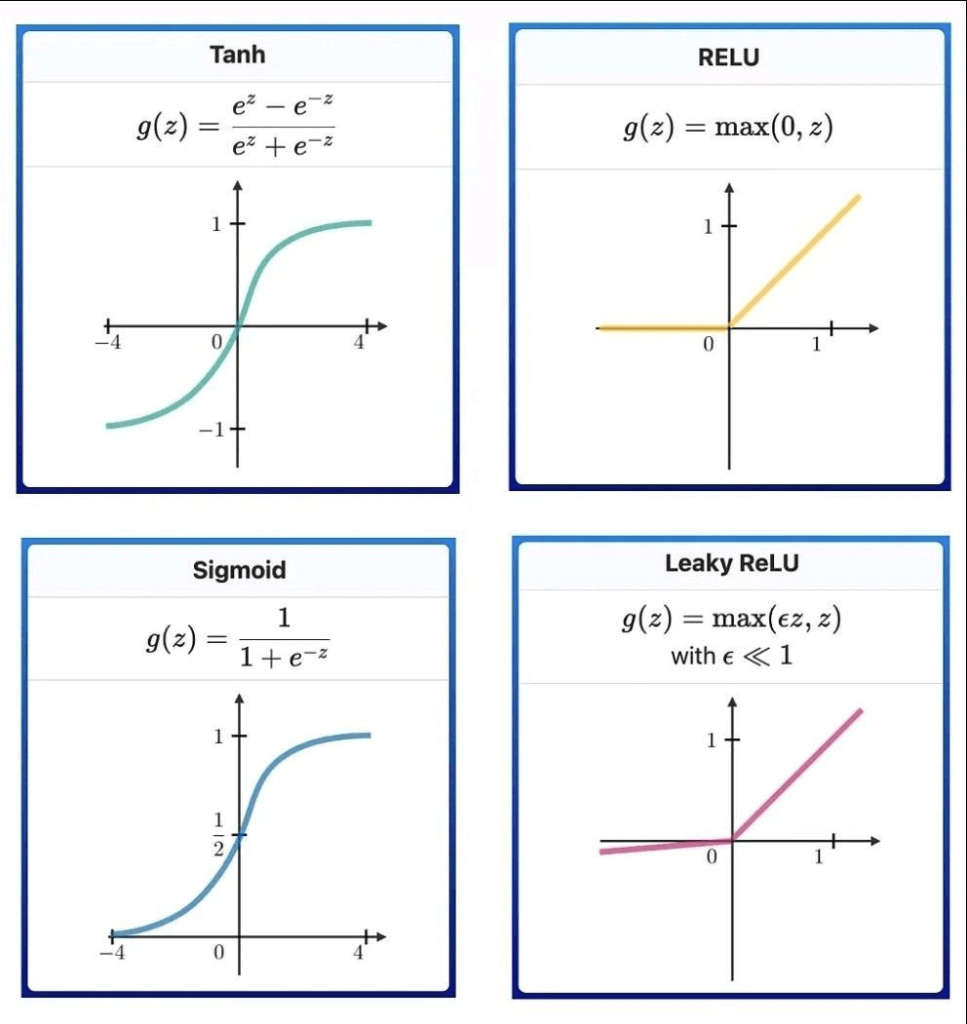
Neural networks are a powerful tool that mimic the human brain's structure and function. These interconnected layers of nodes, called perceptrons, resemble multiple linear regressions. However, the key difference is that perceptrons feed the signal from the regression into an activation function, which can be linear or non-linear.
Mapping Inputs to Outputs
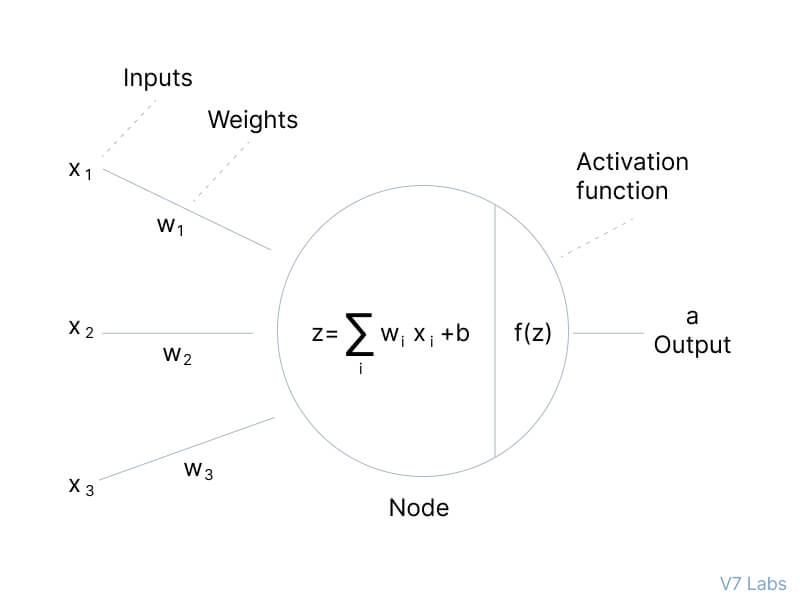
A perceptron receives a vector of inputs, x, consisting of n attributes. These inputs are weighted according to the weight vector, w, similar to regression coefficients. The net input signal, z, is typically the sum product of the input pattern and their weights:
z = ∑(x_i * w_i)
This net input signal, minus a bias b, is then fed into an activation function, f(z), which is usually a monotonically increasing function bounded between -1 and 1.
The Hidden Layers
Perceptrons are organized into layers, with the first layer receiving the input patterns, x, and the last layer mapping to the expected outputs. The hidden layers in between extract salient features from the input data, which have predictive power for the outputs. This feature extraction is similar to statistical techniques like principal component analysis.
Deep Neural Networks
Deep neural networks have a large number of hidden layers, allowing them to extract much deeper features from the data. This has led to their impressive performance in image recognition problems.
Learning Rules: Minimizing Error
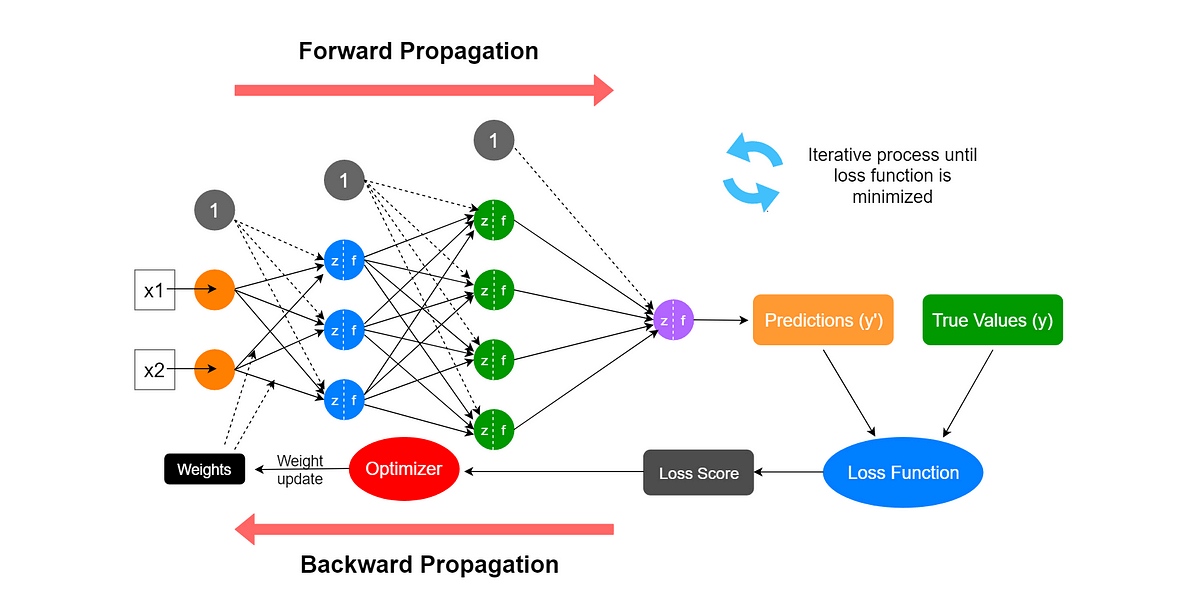
The objective of the neural network is to minimize an error measure, such as sum-squared error (SSE), by adjusting the weights in the network. The most common learning algorithm is gradient descent, which calculates the partial derivative of the error with respect to the weights and updates the weights in the opposite direction of the gradient:
w_new = w_old - η * ∂E/∂w
where η is the learning rate.
Considerations for Neural Networks in Trading
While neural networks are a powerful tool, they do have some limitations. One issue is the assumption of stationarity in the input patterns, which may not always hold true in dynamic markets. Careful consideration of the problem at hand and the appropriateness of neural networks is crucial for successful implementation.
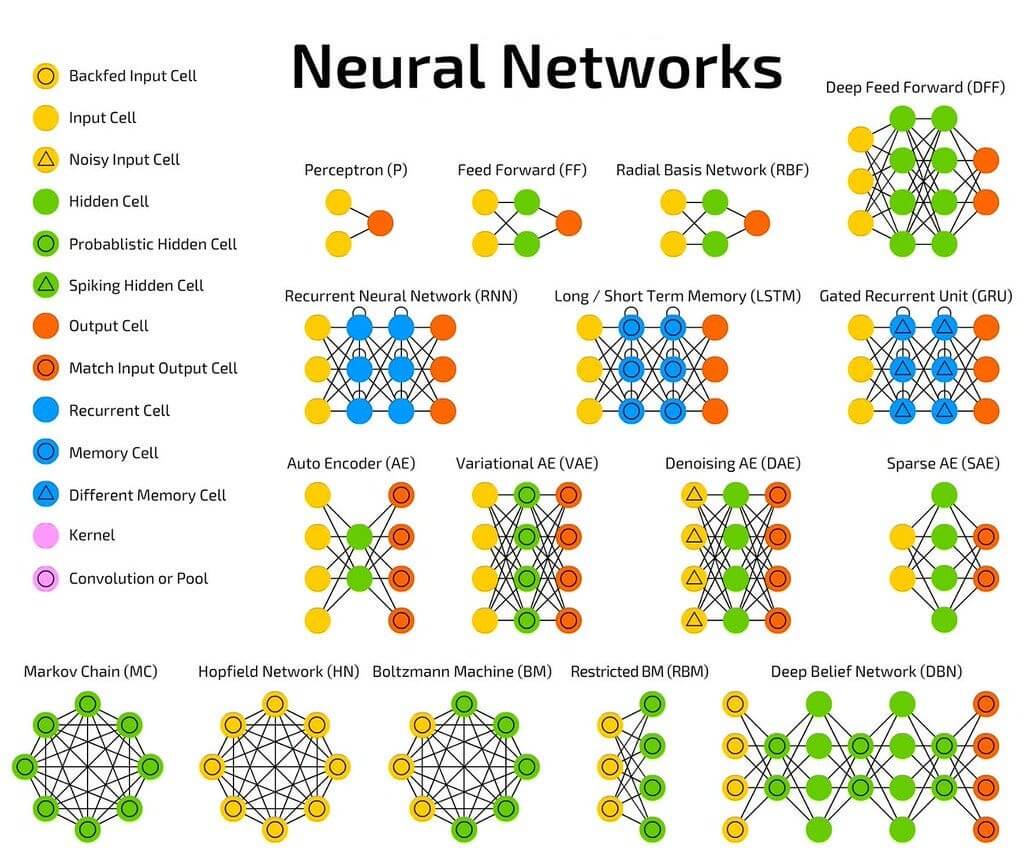
2. Various Architectures of Neural Networks
Neural networks come in a wide array of architectures, and the performance of any neural network is a function of its architecture and weights. While the multi-layer perceptron is the most basic neural network architecture, there are numerous other innovative designs that have been developed over time. As quantitative finance professionals, let's explore some of the most fascinating and powerful neural network architectures and their applications in the financial domain.
Recurrent Neural Networks: Mastering Time-Series Data in Finance
Recurrent neural networks (RNNs) feature some or all connections flowing backwards, creating feedback loops within the network. These networks are believed to perform better on time-series data, making them particularly relevant in the context of financial markets. RNNs, such as the Elman neural network, Jordan neural network, and Hopfield single-layer neural network, have shown promising results in modeling and forecasting financial time-series data, including stock prices, exchange rates, and interest rates.
Neural Turing Machines: Combining Memory and Recurrence for Complex Financial Tasks
A more recent innovation is the Neural Turing Machine, which combines a recurrent neural network architecture with memory. These networks have been shown to be Turing-complete and can learn complex algorithms, such as sorting. In the realm of quantitative finance, Neural Turing Machines could potentially be used for tasks like portfolio optimization, automated trading strategy development, and complex risk management simulations.
Deep Neural Networks: Revolutionizing Financial Image and Voice Recognition
Deep neural networks, with multiple hidden layers, have become increasingly popular due to their remarkable success in image and voice recognition tasks. In finance, these architectures, including deep belief networks, convolutional neural networks, deep restricted Boltzmann machines, and stacked auto-encoders, have found applications in areas such as automated financial document analysis, sentiment analysis of financial news, and voice-based trading assistants.
Adaptive Neural Networks: Optimizing for Non-Stationary Financial Markets
Adaptive neural networks can simultaneously adapt and optimize their architectures while learning. This is particularly valuable in financial markets, which are often non-stationary, as the features extracted by the neural network may change over time. Techniques like cascade neural networks and self-organizing maps can help quantitative finance professionals develop more robust and adaptable models for tasks like market forecasting, portfolio management, and risk analysis.
Radial Basis Networks: Powerful Function Interpolation in Finance
While not a distinct architecture, radial basis function neural networks use radial basis functions, such as the Gaussian distribution, as their activation functions. These networks have a higher information capacity and are often used for function interpolation, including in the kernel of Support Vector Machines. In quantitative finance, radial basis networks have found applications in areas like derivatives pricing, credit risk modeling, and financial time-series forecasting.
When working with neural networks in quantitative finance, it is crucial to test multiple architectures and consider combining their outputs in an ensemble to maximize investment performance.
3. Learning Strategies in Neural Networks
Neural networks can leverage one of three learning strategies: supervised learning, unsupervised learning, or reinforcement learning. As an expert in the field, let's explore these strategies and their applications in the world of finance.
Supervised Learning. Leveraging Labeled Data
Supervised learning requires at least two datasets: a training set with inputs and expected outputs, and a testing set with inputs and unknown outputs. Both datasets must consist of labeled data, where the target is known upfront. This strategy is well-suited for tasks where the desired output is clearly defined, such as predicting financial instrument returns or forecasting economic indicators.
Unsupervised Learning. Discovering Hidden Structures
Unsupervised learning strategies are typically used to uncover hidden structures, such as hidden Markov chains, in unlabeled data. One of the most popular unsupervised neural network architectures is the Self-Organizing Map (SOM), also known as the Kohonen Map. SOMs construct an approximation of the probability density function of an underlying dataset while preserving the topological structure of that data. This can be particularly useful for dimensionality reduction and visualization of financial time series data.
Reinforcement Learning. Optimizing for Desired Outcomes
Reinforcement learning strategies consist of three key components: a policy that specifies how the neural network will make decisions, a reward function that distinguishes good from bad outcomes, and a value function that specifies the long-term goal. In the context of financial markets and game-playing, reinforcement learning can be highly effective, as the neural network learns to optimize a specific measure of risk-adjusted return.
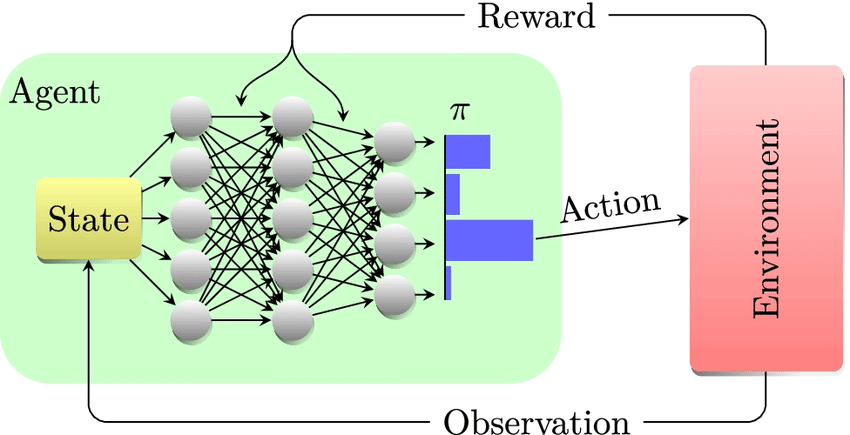
Choosing the Right Learning Strategy
The choice of learning strategy depends on the nature of the problem and the available data. Supervised learning is well-suited for tasks with clearly defined outputs, while unsupervised learning excels at uncovering hidden structures in unlabeled data. Reinforcement learning is particularly powerful in dynamic environments, such as financial markets, where the neural network can learn to optimize for desired outcomes.
Ultimately, the success of a neural network in finance depends on the careful selection and combination of these learning strategies, as well as a deep understanding of the domain-specific challenges and constraints. By leveraging the strengths of each approach, quantitative finance professionals can unlock the full potential of neural networks in their pursuit of superior investment performance.
4. Adapting Neural Networks for the Dynamic Financial Landscape
As an expert in the field, I understand that even after successfully training a neural network for trading, it may stop working over time. This is not a reflection on the neural network itself, but rather an accurate representation of the complex and dynamic nature of financial markets.
The Challenge of Non-Stationarity
Financial markets are complex adaptive systems, constantly evolving and changing. What worked yesterday may not work tomorrow. This characteristic, known as non-stationarity or dynamic optimization problems, poses a significant challenge for neural networks, which are not particularly adept at handling such dynamic environments.
Two Approaches to Adapt
To address this challenge, two approaches can be employed:
- Continuous Retraining: Regularly retraining the neural network can help it adapt to the changing market conditions. This ensures the model remains relevant and responsive to the latest trends and patterns.
- Dynamic Neural Networks: These neural networks are designed to "track" changes in the environment over time and adjust their architecture and weights accordingly. They are inherently adaptive, making them more suitable for dynamic problems.
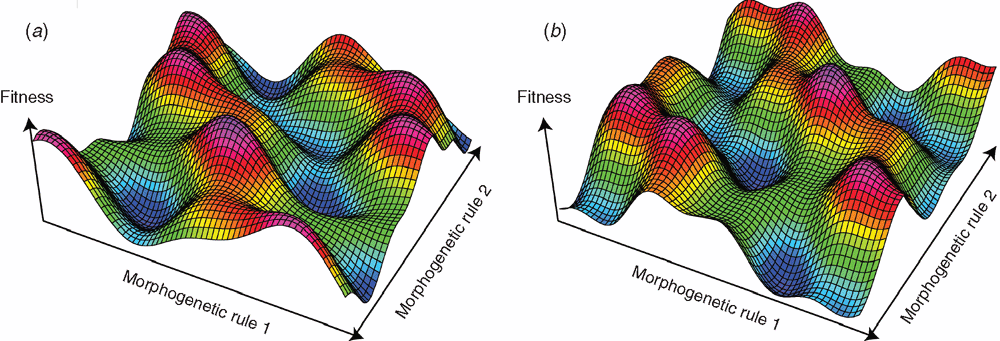
Leveraging Meta-Heuristic Optimization Algorithms
For dynamic problems, such as those present in financial markets, multi-solution meta-heuristic optimization algorithms can be used to track changes in local optima over time. One such algorithm is the multi-swarm optimization algorithm, a derivative of the particle swarm optimization. Additionally, genetic algorithms with enhanced diversity or memory have also been shown to be robust in dynamic environments.
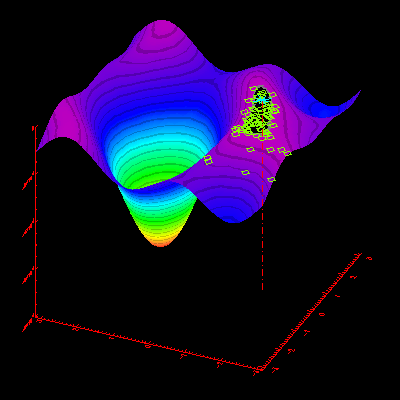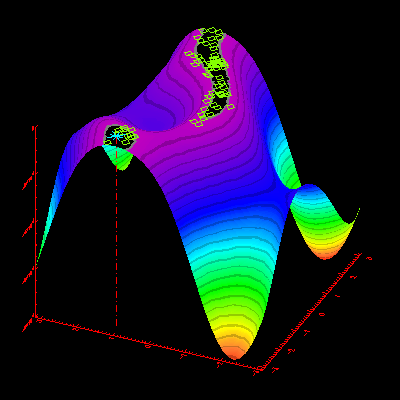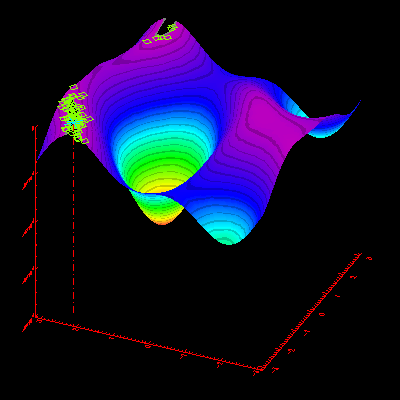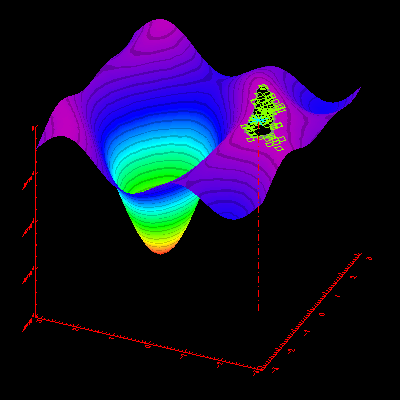
Illustrating the Challenge of Trade Crowding
The illustration below demonstrates how a genetic algorithm evolves over time to find new optima in a dynamic environment. This also mimics the phenomenon of "trade crowding," where market participants flock to a profitable trading strategy, thereby exhausting trading opportunities and causing the strategy to become less profitable.
By understanding the dynamic nature of financial markets and employing adaptive neural network architectures, along with robust optimization algorithms, quantitative finance professionals can better navigate the ever-changing landscape and maintain a competitive edge.
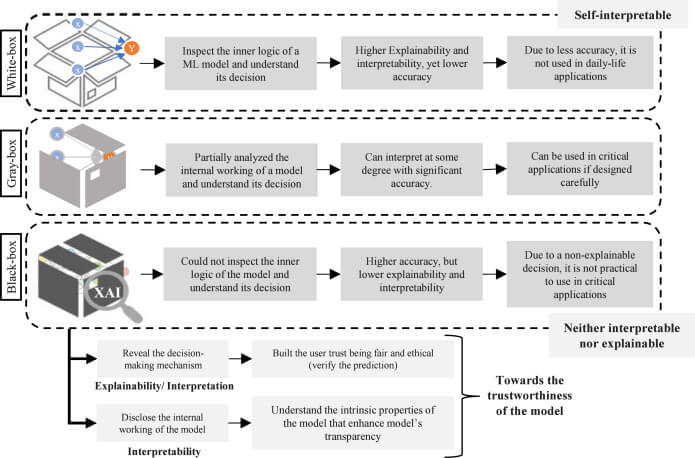
5. Extracting Insights from Black Box Neural Networks
Neural networks are often perceived as black boxes, making it challenging for users to understand and justify their decision-making processes. This presents a significant hurdle for industries like finance, where transparency and explainability are crucial. However, state-of-the-art rule-extraction algorithms have been developed to shed light on the inner workings of neural networks.
Fortunately, the emergence of state-of-the-art rule-extraction algorithms has provided us with a remarkable opportunity to unveil the hidden logic within neural networks. By applying these techniques, we can extract knowledge in the form of mathematical expressions, symbolic logic, fuzzy logic, or decision trees, allowing us to bridge the gap between the neural network's inner workings and the user's need for transparency.
Propositional Logic: Decoding Discrete Decisions
Propositional logic, with its ability to deal with discrete-valued variables and logical operations, offers a powerful means of extracting easily interpretable rules from neural networks. For instance, we can translate the neural network's decision-making process into a set of "IF-THEN" statements, where variables like "BUY," "HOLD," or "SELL" are combined using logical connectives such as OR, AND, and XOR. This level of explainability is crucial for satisfying regulatory requirements and fostering trust among our stakeholders.
Fuzzy Logic: Embracing Nuanced Decision-Making
While propositional logic provides a straightforward approach, the real world often demands a more nuanced understanding of decision-making. This is where fuzzy logic comes into play, allowing us to capture the degree of membership a variable has within a particular domain. By integrating neural networks and fuzzy logic, we can develop Neuro-Fuzzy systems that offer confidence-based decision-making, better reflecting the complexity of financial markets.
Decision Trees: Visualizing the Decision-Making Process
The extraction of decision trees from neural networks, known as decision tree induction, offers a compelling way to present the underlying logic in a visually intuitive manner. These decision trees provide a clear and easily comprehensible representation of how decisions are made based on specific inputs, empowering our users to understand and validate the neural network's decision-making process.
By embracing these rule-extraction techniques, we can unlock the full potential of neural networks while maintaining the transparency and explainability that our industry demands. This approach not only builds trust among our stakeholders but also enhances regulatory compliance and enables more informed and responsible decision-making – crucial elements in the dynamic and highly regulated world of quantitative finance.
Conclusion
Neural networks are a highly versatile and powerful class of machine learning algorithms that have found numerous applications in quantitative finance. However, their success is often hindered by common misconceptions about how they work.
As this article has demonstrated, neural networks are not simply crude imitations of the human brain, nor are they just a "weak form" of statistics. They represent a sophisticated abstraction of statistical techniques and come in a wide variety of complex architectures tailored for different problem domains.
While larger neural networks do not always outperform smaller ones, the key is finding the right architecture and size for the task at hand. Additionally, neural networks can be trained using a variety of optimization algorithms beyond just basic gradient descent.
By understanding these intricates of neural networks, finance professionals can harness their true power to build robust, high-performing models and trading strategies. The road to success with neural networks requires a deep understanding of their foundations and limitations, but the rewards can be substantial for those willing to invest the time and effort.