Solving Complex Issues by Applying Mathematical Thinking through Fractal Patterns
12 December, 2023
Ever wonder what it's like finding something no one else has ever seen? Exploring the Mandelbrot Set, you can do just that.
This fractal frontier reveals endless new shapes at every scale.Over 100 billion images have offered novel insights, yet an estimated 10 to the power of 100,000 more designs hold undiscovered revelations.
Like exploring the intricate patterns revealed in fractals at increasing magnitudes, considering issues from alternative angles often exposes aspects that remain obscured with a single outlook. Each novel approach brings fresh perception, analogous to peering deeper into an inexhaustible fractal and approaching challenges from different perspectives allows us to discover new insights.
Rethinking Complexity through Fractal patterns
Knowledge is something that humans have sought to understand since the beginning of time. But our conceptions of knowledge are not static - they evolve as our world changes and new perspectives emerge. What does it really mean to "know" something? Is knowledge just facts, or something more? As technology changes our lives at warp speed, old ideas get questioned while whole new ways of thinking emerge. In these dynamic times, reexamining what we assume is more important than ever. That's where fractals come in - their intricate yet simple patterns across scales.
Fractals repeating intricacy across scales mirrors how addressing part of a complex problem impacts the whole. Now researchers apply this fractal thinking in fields from epidemiology to economics. By zooming in and out of multiple perspectives like exploring a fractal, they solve issues thought intractable.

Fractals also teach iterating on solutions, as a nuanced shift rearranges understanding exponentially. This bending of conventional "wisdom" inspires original solutions. As with fractals, peeling back the layers of difficult problems reveals fresh order ripe for application.
The Infinite Beauty of Fractals
Fractals are truly unique mathematical constructs that display intricate patterns no matter how close you look. Dubbed "infinitely complex patterns" by mathematician Benoit Mandelbrot who discovered them, fractals hold surprises at every level of magnification.

Zoom out fully and you see an beautiful overall shape, but zooming in reveals astonishing fine-scale intricacy that seems to go on forever. No matter how far you peer into a fractal form, further magnification always allows discovery of even smaller nested details.
It's mind-boggling to think fractal geometry possesses this multi-scale quality with no discernible smallest component. Their designs are preserved flawlessly from macro to micro, granting fractals visual complexity across infinite scales.
Fractals impart a profound sense of nature's endless potential for exquisite ordered chaos. They remind us that miraculous intricacy can be hidden within seemingly simple patterns, just awaiting humanity's commitment to ever-deeper observation and understanding. Fractals showcase math's perennial ability to uncover reality's deepest wonders through dedication to detailed investigation without limits. True beauty, it seems, lies in apprehending wonders that have no smallest part.
Ever-Present Mandelbrot Universal Fractal Pattern
The Mandelbrot set is surprisingly common in math! No matter how you tweak the equation for this fractal shape, it always looks the same.
To understand the Mandelbrot set, we start with a simple quadratic equation: z*n+1 = z*n^2 + c.
This equation takes a starting value z0 and plots it, then plugs the result back in and plots again, and so on. We test different complex numbers for "c" to see if the plotted values stay bounded or fly off to infinity. Numbers that remain bounded belong to the Mandelbrot set.
For example, with c = 1:
z0 = 0
z1 = 02 + 1 = 1
z2 = 12 + 1 = 2
z3 = 22 + 1 = 5
...
You can see the values get bigger really fast, shooting off to infinity. So c = 1 is not part of the set.
But with c = -1:z0 = 0
z1 = 0−1 = -1
z2 = (-1)2 − 1 = 0
z3 = 02 − 1 = -1
...
The values bounce between 0 and -1, staying nice and bounded. Therefore, c = -1 is inside the Mandelbrot set. Through testing inputs like this, we map out the famous fractal shape - all from a simple repeating quadratic process.
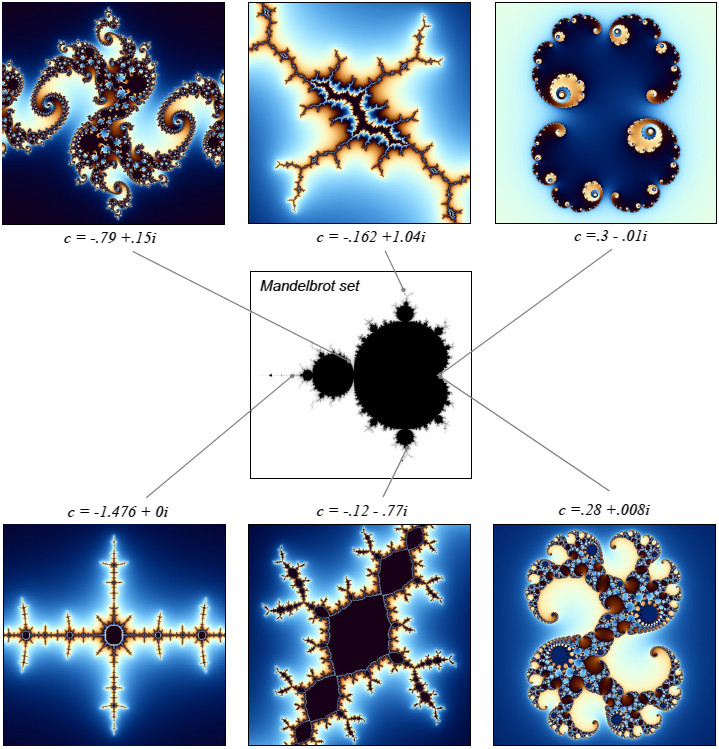
The standard mathematical Mandelbrot equation is: z = z^2 + c. This plots points on the complex plane, building the fractal shape we all know. But scientists found that even when changing this formula, like z = k1*z^2 + k2 + c, the Mandelbrot pattern stays exactly the same. They could multiply z by any number, add any other complex number, and nothing changed - it still gave the famous Mandelbrot set! This shows how robust and flexible the equation is.
Scientists think this happens because the Mandelbrot set acts as a foundation. A bit like how pi and e are core math constants, the Mandelbrot is key to shapes made by repetitive complex equations. No matter how you stretch, spin or alter the starting rule, that foundational Mandelbrot pattern holds strong.
It's cool that such a small equation creates a shape so universal! The Mandelbrot set really must tap into something fundamental about how complex numbers repeat and build on each other. Even with changes, its iconic form always emerges to remind us of the deep math hiding in simple ideas.
Fractals and the Infinite Complexity of Knowledge
When it comes to knowledge, fractals reveal there's always more to discover. Just like the intricate patterns that unfold within fractals like the Mandelbrot set, knowledge has a hidden infinite complexity.
Benoit Mandelbrot showed us fractals aren't just cool patterns - they demonstrate how simple rules can create never-ending depth and connections. The same is true of what we know. Zooming into any topic reveals deeper layers of understanding, just like the boundless details within fractals.

Knowledge mirrors fractals' self-similarity too. Further exploration often uncovers remarkably similar patterns at increasingly granular levels. And just as pieces of fractals fit together in complex nested hierarchies, ideas in different fields interconnect in ways we're still piecing together.
Trying to map the borders of our knowledge is futile, just as fencing in a fractal leads nowhere. Wherever we peer closer, blurred edges dissolve to expose entirely new landscapes waiting in the fog. Our current view gives but a glimpse of knowledge's real magnificence.
Infinite richness spans disciplines without clear lines dividing them. Knowledge weaves as one fractal tapestry, not a jumble of separate facts. By embracing this fractal reframing, entirely new perspectives emerge. There are always deeper dimensions to explore - so keep your mind open to discoveries beyond the horizon.

Tackling Complex Problems Like a Fractal
When faced with a complex problem, it helps to view it like exploring a fractal - starting broad and zooming in over time.
Look at the big picture first. Ask questions to understand the overall shape of the problem. What are the core issues? How do they relate? This high-level perspective provides valuable insights.
Drill into interesting areas. Answering initial questions will likely spark 3-5 new questions. Don't shy away from diving deep into particularly puzzling parts of the problem. Further investigation could unlock answers.
Patterns emerge on deeper dives. As with fractals, self-similarity often appears. Themes from one area resonate elsewhere. Leverage these "echoes" between sub-problems for new solutions.
Know when to zoom out or change focus. If analysis feels repetitive, zoom back out to confirm understanding before determining next steps. New information may also suggest a tangent worth exploring instead. Stay nimble!
Tackling complex issues like fractals takes patience and perseverance. Starting broadly and iteratively honing your focus produces the clearest perspective. Don't fear diversions - unexpected insights can come from any level. With this iterative approach, even the most multi-faceted problems can be solved!
The Power of Admitting What You Don't Know
Most of us pride ourselves on what we understand, but there is power in acknowledging our ignorance. His chapter suggests the boundaries of our knowledge are just as important to define as our comprehension.
The ignorance plays 3 key roles:
1. It highlights gaps and inconsistencies. Not knowing something shows where further inquiry is needed. This motivates additional learning and discovery.
2. It prevents dogmatism. Admitting limited understanding discourages overconfidence that can stand in the way of progress.
3. It defines frontiers. Our ignorance illuminates mysteries and anomalies that represent new opportunities to expand fields of study.
He cites 2 important examples:
Scientific revolutions often follow periods where prevailing theories were known to be incomplete.
Progress relies on celebrating the unknown, not pretending we fully comprehend topics.
In summary, ongoing ignorance is the driver of our perpetual quest to better understand the world around us. As Socrates knew, the wisest among us acknowledge the limits of human understanding. The next time you feel proud of what you know, consider adding what you don't know yet - it just might spark your greatest insights.