The Geometry of Price: Quantitative Pattern Discovery with Soft-DTW in Bitcoin
In crypto markets where narratives shift hourly and prices rarely move in straight lines, identifying repeatable structure feels impossible. But what if you had a tool that decoded it?
Retail participation, social-driven price action, and the rise of algorithmic trading have influenced how people engage with assets like Bitcoin. In this increasingly competitive and volatile environment, smart decision-making requires more than intuition. You need tools that adapt to the data, recognize patterns beneath noise, and work across timeframes. One such tool is Dynamic Time Warping (DTW).
In this article I introduce DTW and its enhanced variant, Soft-DTW, as shape-aware distance measures that can uncover structure in noisy, nonstationary markets like crypto. We'll walk through how DTW works—mathematically and conceptually—why it outperforms traditional similarity measures for time series like price action, and whether it can help cluster, interpret, and even predict Bitcoin price movements.
By the end, you’ll have both the theoretical grounding and the practical evidence for using DTW in crypto market analytics.
How DTW Bends Time to Find Patterns
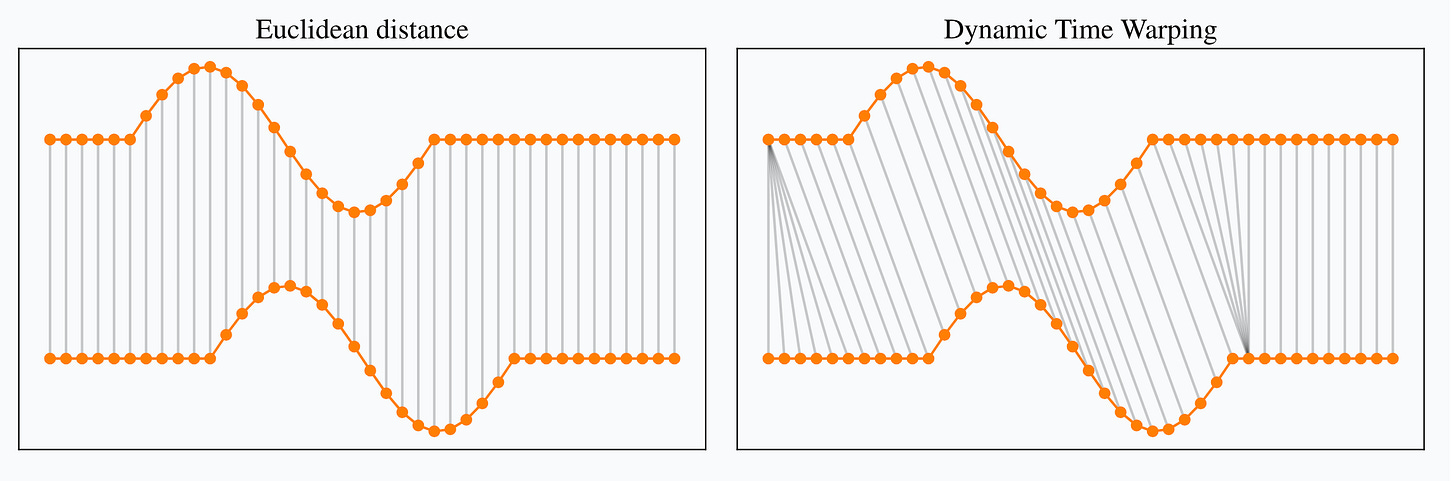
Let’s start with a common pitfall: most financial analysis relies on tools like correlation or Euclidean distance. These are simple to compute and often intuitive. But they make a big assumption—that price patterns align perfectly in time. That’s rarely true in markets like crypto, where noise, lag, and structural breaks are everywhere.
Correlation gives you a single number summarizing how two series move together, but it can’t distinguish whether one lags the other. Euclidean distance, on the other hand, assumes two time series are perfectly aligned. A pattern that’s just slightly delayed—or speed-shifted—can be seen as “far away” when it's actually quite similar.
DTW addresses this by non-linearly aligning the time axes of two sequences. You can think of it as letting two patterns “stretch” or “compress” so they match in shape, even if they unfold at different speeds.
Mathematics of DTW
Let’s define two time series:
We want to compute the distance between these series by aligning them in a way that minimizes the total mismatch.
First, create a cost matrix Δ, where each element is:
\( \Delta(i, j) = d(x_i, y_j) + \min \begin{cases} \Delta(i-1, j), \\ \Delta(i, j-1), \\ \Delta(i-1, j-1) \end{cases} \)
Here, 𝑑(𝑥_𝑖 , 𝑦_𝑗) is usually squared difference.The recursion builds a dynamic programming matrix. The final DTW distance is the cost at Δ(𝑚, 𝑛).
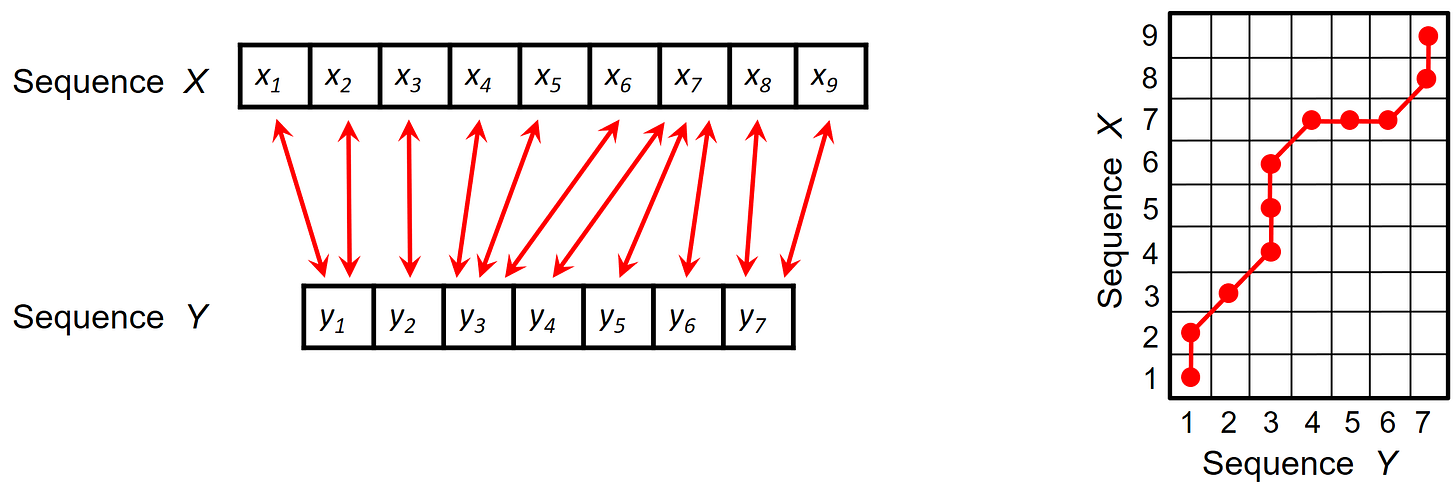
From this matrix, extract the warping path 𝑤 = [(𝑖_1 , 𝑗_1) , . . , (𝑖_𝐿 , 𝑗_𝐿)] satisfying:
Boundary conditions: 𝑤_1 = (1,1) , 𝑤_𝐿 = (𝑚, 𝑛)
Monotonicity: indices don’t decrease
Continuity: steps are local (you can only move right, down, or diagonally)
This warping path minimizes the total alignment cost. What you get is not a rigid pointwise match, but an elastic alignment.
The beauty is that DTW recognizes shape, not position.
Soft-DTW: A Smoother Version for Learning
Standard DTW has a problem: it’s non-differentiable, which makes it hard to optimize in machine learning. Enter Soft-DTW, a differentiable version introduced by Cuturi and Blondel (2017).
Soft-DTW replaces the hard min operator with a softmin function:
This gives you a smooth approximation of the min, where controls the smoothing. When , Soft-DTW becomes standard DTW. When , it averages everything.
This smoothing allows Soft-DTW to be used as a loss function in gradient-based optimization—ideal for clustering, forecasting, or neural network training.
From Patterns to Prediction
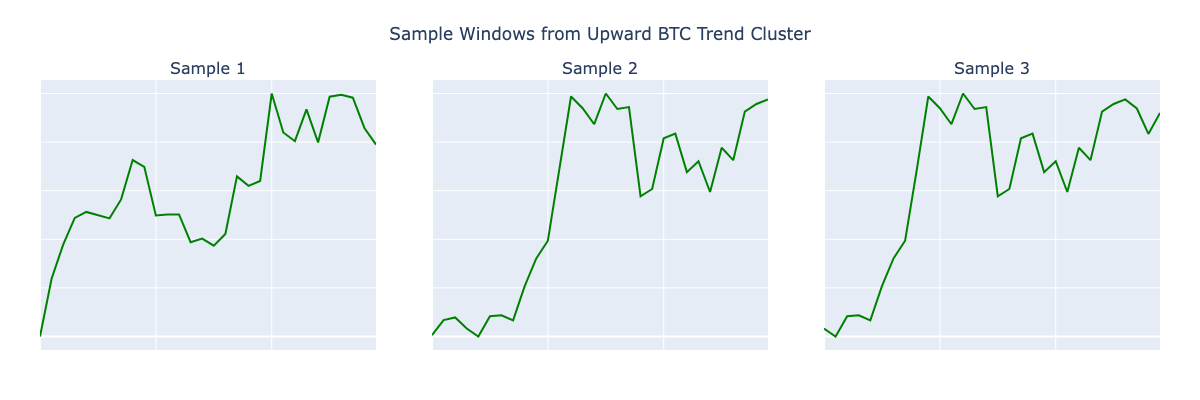
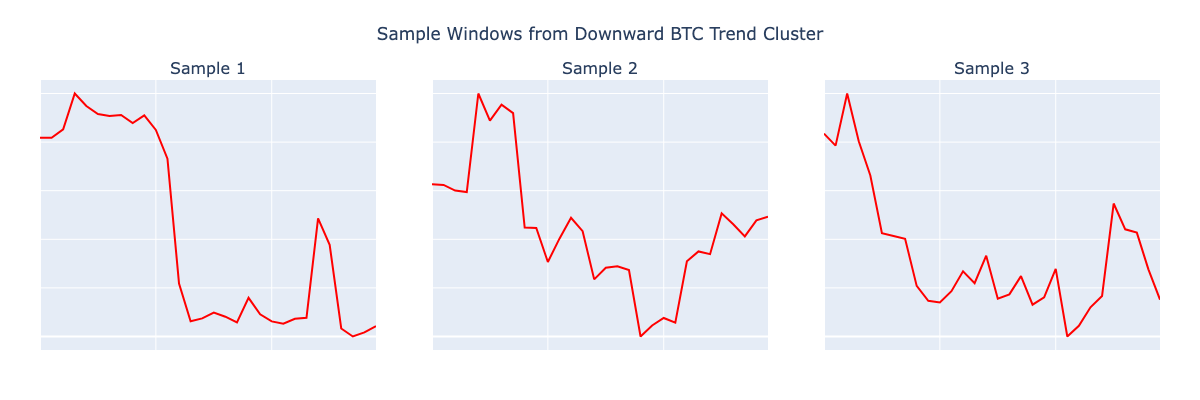
If Soft-DTW can group price shapes, can it also tell us what happens next? Early results say yes—and the signals are cleaner than most technical indicators. Below are sample patterns it successfully clustered into rising and falling price structures.
But this kind of result need a carefully tuned setup to avoid overfitting while still generalizing to unseen data.
Next, I’ll walk you through the full experiment—how I built the dataset, set the parameters, and trained a shape-aware prediction engine that actually works.